Optimisation de l'empreinte carbone de charge de batteries
Avec l’accroissement de la part des énergies renouvelables non pilotables dans les systèmes électriques, l’intensité des émissions de CO$_2$ dues à la production d’électricité devient de plus en plus variable. En été, l’intensité carbone est faible en journée, lorsque l’énergie solaire est abondante. En hiver, elle diminue pendant les périodes de vent. En soirée, l’intensité carbone est souvent à son comble, car les moyens de production bas-carbone ne suffisent pas à couvrir la demande.
Ainsi, l’empreinte carbone de l’électricité consommée varie d’une heure à l’autre. Pour cette raison, il est plus ou moins opportun de, par exemple, charger une batterie selon le moment de la journée. Or la charge des batteries (de voiture, de vélo ou tout autre objet) peut souvent être reportée dans un temps raisonnable, plutôt que d’appeler du courant dans des moments où les moyens de production thermiques fortement émetteurs de carbone sont nécessaires pour faire face à la consommation. Par exemple, si je dois recharger mon vélo électrique pour après-demain, autant le charger lorsque cela ne nécessitera pas d’appeler des centrales à gaz.
Pour cela, j’ai conçu une prise électrique qui optimise la charge d’une batterie quelconque (voiture, vélo, ordinateur, etc.) de sorte à minimiser l’empreinte carbone due à la charge. Les paramètres de charge seront configurables via un boîtier, avec un affichage LCD pour faciliter le réglage et le suivi de la charge.
Sommaire de la page
Démonstrations
Voici quelques démonstrations (on aperçoit la prise électrique pilotée par l’Arduino, la lumière rouge indiquant lorsque celle-ci est active).
Commande forcée (sans optimisation)
Commande optimale (avec optimisation)
Affichage du programme de charge
Cahier des charges
Paramètres réglables
Le temps de charge minimum (entre 1h et 48h). C’est le temps pendant lequel la charge doit être active pour atteindre le niveau de charge désiré.
La durée maximale de la charge (entre 1h et 48h). Au bout de cette durée la charge doit être achevée.
Affichage LCD
L’affichage LCD doit remplir les fonctions suivantes:
Réglage des différents paramètres
Progrès de la charge estimé
Estimation des émissions de CO2 épargnées
État de la charge (ON/OFF/pause) et programme de charge
Solution technique
Le principe de fonctionnement est le suivant :
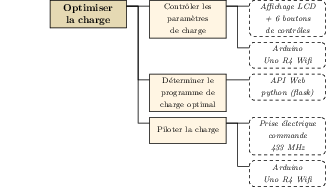Figure 1. Diagramme FAST
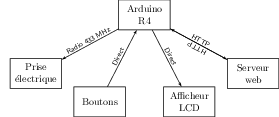Figure 2. Schéma simplifié de la solution
Composants techniques
1x Arduino UNO R4 WiFi
1x SHIELD-LCD 16x2 avec 6 boutons de réglage (gauche, droite, haut, bas, ok, reset)
1x Prise électrique commandée à distance (433 MHz)
Programme de charge optimal
Je commence par l’API web qui va calculer le programme de charge optimal, qui est le coeur du projet. Les calculs nécessitent de combiner des informations très récentes et diverses, et pour cela il est plus commode de les déléguer à une machine puissante et sophistiquée. Je propose donc un serveur web disponible 24h/24, 7j/7, auquel l’Arduino communique les paramètres de charge via Wifi, et qui renvoie en réponse un programme de charge optimisé.
Fonction de coût et optimisation
Le programme de charge optimisé est déterminé par la minimisation d’une fonction de coût, étant donné deux paramètres :
Le temps de charge nécessaire pour charger la batterie au niveau désiré, $\tau$
Le temps maximal de charge $T$ (après un temps $T$, la charge doit être impérativement finie).
Soit $I(t)\in \{0,1\}$, la commande de l’interrupteur au cours du temps. Pour accomplir la charge sur une plage de durée maximale $T$, il faut que la charge soit active pendant un temps $\tau$, c’est-à-dire :
\[\displaystyle\int_0^{T} I(t) dt \geq \tau\]Autrement dit, $T$ et $\tau$ imposent une contrainte sur $I(t)$.
Soit maintenant une fonction de coût $C(I)=\int_0^{T} p I(t)c(t)dt$ où $c(t)\geq 0$ est le débit de CO$_2$ émise par un watt supplémentaire d’électricité consommé sur le réseau à l’instant $t$, et $p$ la puissance de charge (supposée constante). On chercher à minimiser cette fonction de coût, c’est-à-dire à trouver $I(t)$ tel que:
\[\begin{aligned} I &= \mathop{\mathrm{arg\,min}}_{I:[0,T]\to\{0,1\}} \int_0^{T} p I(t) c(t) dt\\ \tau &\leq \displaystyle\int_0^{T} I(t) dt\end{aligned}\]Si $p$ est constant, alors il ne reste plus qu’à déterminer la fonction de coût $c(t)$ pour choisir un programme optimal.
L’estimation du coût instantané $c(t)$ requiert une prédiction de l’intensité carbone de la grille électrique jusqu’à $t+T$ où $T$ peut atteindre 48h. Cela nécessite de prédire:
La courbe de consommation
La courbe de disponibilité des divers moyens de production
Une modélisation de l’activation des moyens de production en fonction de leur disponibilité et de la consommation
Il s’agit d’une modélisation du système électrique français comme un tout homogène, ce qui est une approximation forte, mais on peut supposer que l’intensité carbonne de la consommation électrique est très corrélée à travers la France métropolitaine.
Estimation de la consommation
Pour la courbe de consommation, j’exploite les prévisions de consommation de RTE à 48 heures. Celles-ci tiennent compte de facteurs comme la thermosensibilité de la demande (par exemple, en hiver, plus il fera froid, on s’attend à une demande élevée).
Estimation de la disponibilité
Pour la courbe de disponibilité (la puissance délivrable à chaque instant pour chaque source, en MW), j’utilise différentes stratégies. Pour le solaire et l’éolien, j’exploite les prévisions de production de RTE, qui intègrent les prévisions météo. Pour l’hydraulique, ces prévisions n’existant pas à ma connaissance, je sépare plusieurs cas :
L’hydraulique “au fil de l’eau”: je suppose que la production i) exploite la totalité du flux d’eau disponible; ii) que celui-ci évolue lentement sur une échelle de temps de deux jours, de sorte que la production demain et après-demain est environ égale à la production constatée aujourd’hui.
L’hydraulique “réservoirs” (les lacs de barrage). La disponibilité est égale à la capacité installée.
L’hydraulique “stockage”: pour l’instant non modélisé.
Pour toutes les autres sources (nucléaire, biomasse, gaz, charbon, etc.), la disponibilité est calculée comme la capacité installée moins le total des capacités prévues d’être indisponibles à j-2 selon les prévisions de RTE.
Mécanisme d’allocation des sources de production
Enfin, reste à modéliser, à partir de prévisions de consommation et de disponibilité, quelles sources seront activées pour répondre à la demande au cours du temps. Pour cela je suppose que toutes les unités d’un même mode de production ont le même coût de marginal production, ce qui est inexact mais a priori relativement réaliste (à vérifier). Soit $P_{i,t}$ la puissance produite une source $i$ à l’instant $t$, $P_{i,t}^{\text{max}}$ la puissance maximum disponible pour cette source, et $c_i$ son coût marginal de production. Si de plus $D_t$ est la demande totale à l’instant $t$, alors l’allocation optimale des modes de production est donnée par :
\[\begin{aligned} (P_{i,t}) &= \mathop{\mathrm{arg\,min}}_{ (P_{i,t})\in\mathbb{R}^n } \sum_{i=1}^n P_{i,t} c_i\\ 0 &\leq P_{i,t} \leq P_{i,t}^{\text{max}}\\ \sum_{i=1}^n P_{i,t} &= D_t\end{aligned}\]Il existe une solution dès lors que $\sum_{i=1}^n P_{i,t}^{\text{max}}\geq D_t$ à chaque instant $t$. En fait, la solution consiste à exploiter autant que possible la source la moins chère, puis la deuxième source la moins chère, etc., et ce que jusqu’à la source la plus chère en dernier ressort. L’ordre dans lequel sont appelées les sources est appelé “merit order”.
Reste à déterminer les coûts marginaux de chaque mode de production. C’est essentiellement les coûts d’exploitation + le coût du combustible (donc 0 pour une bonne partie des EnR), mais aussi des coûts d’opportunité dès lors qu’une gestion de stock est en jeu. En fait, peu importe les valeur exactes des coûts marginaux, tant qu’elles reproduisent fidèlement le merit order effectif en pratique. Pour l’instant, je me suis contenté de valeurs arbitraires bricolées pour obtenir un résultat à peu près acceptable. Tout est résumé dans le tableau 1.
| Source | Capacité maximale (MW) | Coût minimal (euros/MWh) | Merit order | Calcul de disponibilité |
|---|---|---|---|---|
| Solaire | 13 600 | 0 | 0 | Prévisions de production RTE |
| Éolien | 19 500 | 0 | 0 | Prévisions de production RTE |
| Hydro (fil de l’eau) | 11 514 | 0 | 0 | Production constatée à j-2 |
| Hydro (réservoirs) | 8 787 | 85 | 5 | Capacité totale - indispos |
| Hydro (stockage) | 5 064 | * | NA | * |
| Nucléaire | 61 400 | 10 | 1 | Capacité totale - indispos |
| Biomasse | 2 230 | 70 | 3 | Capacité totale - indispos |
| Gaz | 12 800 | 80 | 4 | Capacité totale - indispos |
| Charbon | 1 820 | 90 | 6 | Capacité totale - indispos |
| Imports | ? | 7 | Virtuellement illimitée |
Tableau 1
En fait, les coûts ne sont pas constants pour toutes les unités de chaque mode de production. Pour tenir compte, j’ai supposé que la fonction de coût d’un mode de production dépend de la puissance produite de façon linéaire :
\[\begin{equation} c_i(P_{i,t}) = c_i^0 (1+\theta_i P_{i,t}) \end{equation}\]Cela revient en gros à supposer que la distribution des coûts de production pour chaque moyen de production est uniforme (comprise entre un minimum et un maximum). Les paramètres $\theta_i$ ont été ajustés aux données en minimisant l’erreur quadratique moyenne du modèle (évalué sur les données de production entre le 1er novembre 2022 et le 1er mars 2023).
Exemples
La figure 3, un exemple basé sur les prédictions du 1er mars 2023 au 3 mars 2023. Le graphique du haut représente la répartition de la production prédite du 1er mars à minuit au 2 mars à 23:59, par tranche de une heure. L’intensité carbone est représentée en noire. Le graphique du bas représente la commande optimale pour trois jeux de paramètres : $(\tau=12\text{ h},T=12\text{ h}), (\tau=12\text{ h},T=24\text{ h}), (\tau=12\text{ h},T=48\text{ h})$. L’optimisation préfère bien les périodes de basse intensité carbone pour la charge, et d’autant plus que $T$ est grand, permettant des programmes de charge plus étalés.
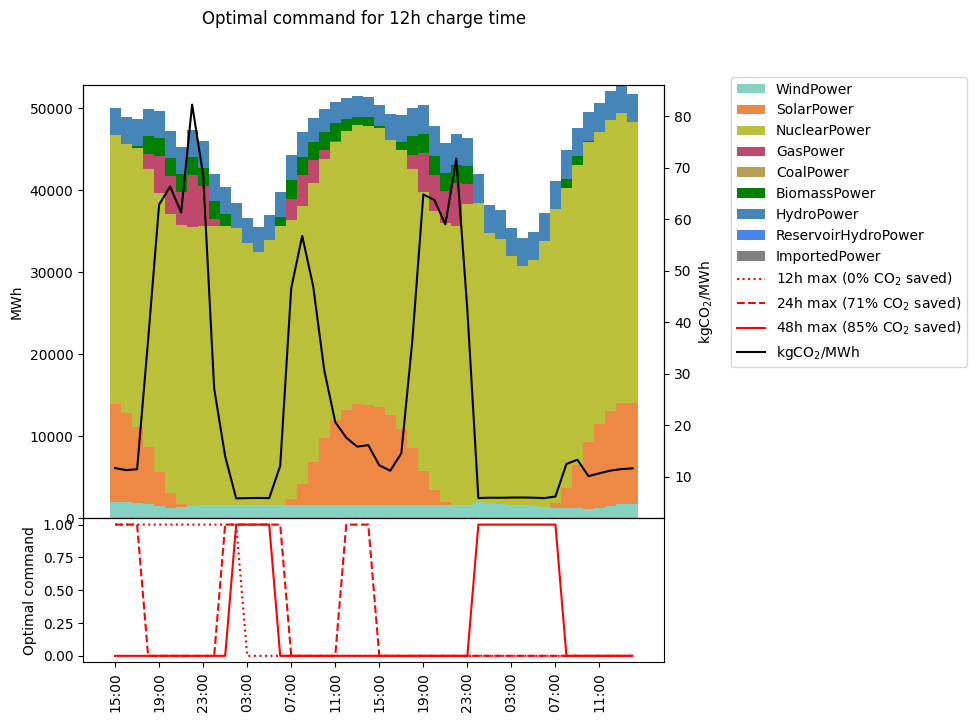Figure 3. Répartition de la production, intensité carbone (en noire) et commande optimale de charge (en rouge, graphique du bas)
Performances
Pour évaluer la performence du modèle, je propose deux stratégies :
- Évaluer la corrélation de Spearman entre l’intensité carbone prédite par le modèle sur les données passées et l’intensité carbone estimée par Electricity Maps pour les journées correspondantes. En effet, le modèle doit pouvoir classer chaque heure entre $t$ et $t+$48h par intensité carbone (prédite) croissante. C’est exactement cette capacité qui est évaluée via le coefficient de Spearman.
- Évaluer les gains obtenus via les commandes de charge prédites, en supposant que l’intensité carbone réelle est celle calculée a posteriori par Electricity Maps.
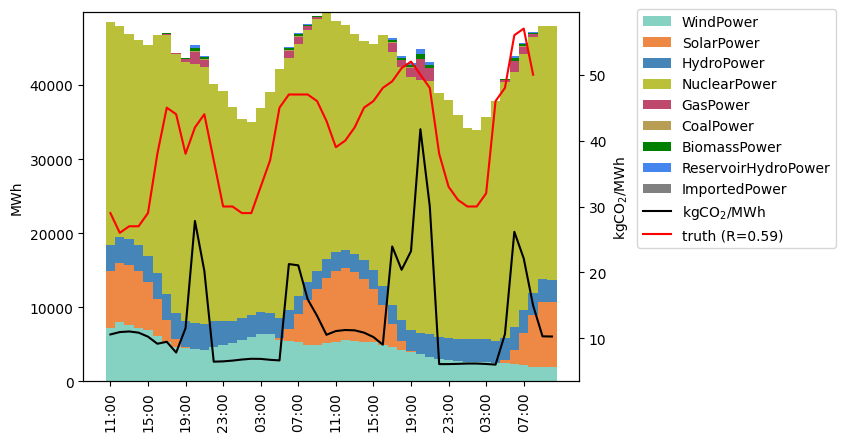Figure 4. Répartition de la production, intensité carbone prédite (en noire) et constatée par Electricity Maps (en rouge). La corrélation de Spearman entre prédiction et réel est d’environ 0,6.
Améliorations de la modélisation prévues
Dans le futur je propose d’effectuer progressivement les améliorations suivantes:
Meilleure prise en compte de la dispersion de la distribution des coûts marginaux à travers les unités d’un même mode de production (non-uniformité)
Modéliser un coût marginal dynamique de l’hydraulique stocké (réservoirs et pompage-turbinage) à travers les coûts d’opportunité associés à la mobilisation du stock.
Prise en compte de la variabilité des coûts marginaux
Prise en compte des temps de montée en charge
Prise en compte de la cogénération
Modélisation les imports, pays par pays, à partir du coût moyen et des émissions de CO$_2$ moyennes mois par mois et heure par heure.
Amélioration de la modélisation de la production hydroélectrique au fil de l’eau, en substituant $P_{t+\Delta t} = P_{t}$ par $P_{t+\Delta t} = P_{t} + \int_0^{\Delta t} h(\tau)\text{précipitations}(t+\Delta t-\tau)\cdot d\tau$ (où $h$ un noyau tel que $h(\tau<)=0$ si $\tau<0$).
L’API python
Je programme l’API python via Flask. Les optimizations sont effectuées via la bibilothèque python cvxpy. Le code est disponible sur Github: https://github.com/lucasgautheron/co2-optimizer.
Celle-ci est hébergée sur une instance EC2. J’utilise Gunicorn+nginx pour le serveur web. J’ai suivi ce tutoriel pour leur configuration.
Programmation Arduino
Le code pour le microcontrolleur est accessible sur Github: ici. Sont implémenté : les menus de configuration, le suivi de charge, la récupération de la commande optimale via http (depuis l’instance EC2), la commande à distance de la prise électrique du chargeur.