Le nucléaire, ‘plus intermittent’ que l’éolien?

Des personnalités politiques de premier plan de la France Insoumise affirment depuis plusieurs mois que le nucléaire est une source d’électricité “intermittente” ¹, et même bientôt “plus intermittent[e] que l’éolien” si l’on en croit Jean-Luc Mélenchon ². Ce discours, bien sûr, vise à promouvoir la transition vers 100% d’énergies renouvelables défendue par le parti. Une telle transition impliquerait de fermer les 56 réacteurs actuellement en opération, lesquels ont fourni à la France 70% de son électricité en 2019 ³. Une telle tâche n’est pas seulement difficile ; elle est aussi critiquable, alors que l’énergie nucléaire demeure à ce stade la source la plus propre en terme de gaz à effet de serre. Alors que le bien-fondé de la sortie du nucléaire en Allemagne est remise en question par les menaces actuelles sur l’approvisionnement en gaz et par ses conséquences en terme d’émissions de gaz à effet de serre, LFI et ses alliés d’EELV ont besoin de renforcer leurs arguments contre l’énergie nucléaire. Par chance pour eux, le parc nucléaire français rencontre actuellement des difficultés majeures. Environ la moitié des réacteurs sont arrêtés pour des opérations de maintenance, pour diverses raisons, y compris le fameux problème de corrosion sous contrainte anormale identifié sur plusieurs d’entre eux. Il en résulte que la disponibilité du parc nucléaire est actuellement très limitée, et un risque de blackout pour cet hiver. C’est principalement sur la base de cette situation que le nucléaire est qualifié d’“intermittent” par la France Insoumise, et même “bientôt plus intermittent que l’éolien”.

Quantifier l’intermittence

Qu’en est-il vraiment ? Pour répondre à cette question encore faut-il savoir ce que l’on entend par intermittent. Par source d’énergie intermittente, pour ma part, j’entends une source d’énergie qui ne garantit pas la livraison d’une quantité de puissance désirée de manière fiable. Peut-on quantifier l’intermittence du nucléaire et de l’éolien en ces termes ? Grâce aux données publiques du mix énergétique français, c’est possible. Ces données comprennent la puissance produite filière par filière et demi-heure par demi-heure entre 2012 et 2021 ⁴; ainsi que la puissance installée par unité de production et leur date de mise en service ⁵. Ces données, une fois combinées, permettent d’estimer la puissance installée nécessaire pour garantir la livrasion d’une quantité de puissance souhaitée avec certain taux de fiabilité (i.e., une certaine fration du temps). Cela permet de répondre à des questions telles que : combien faut-il installer d’éoliennes pour obtenir au moins 1 GW (la puissance typique d’un réacteur nucléaire) 90% de l’année ? Les résultats sont donnés ci-dessous, et la méthodologie est explicitée et discutée plus bas.

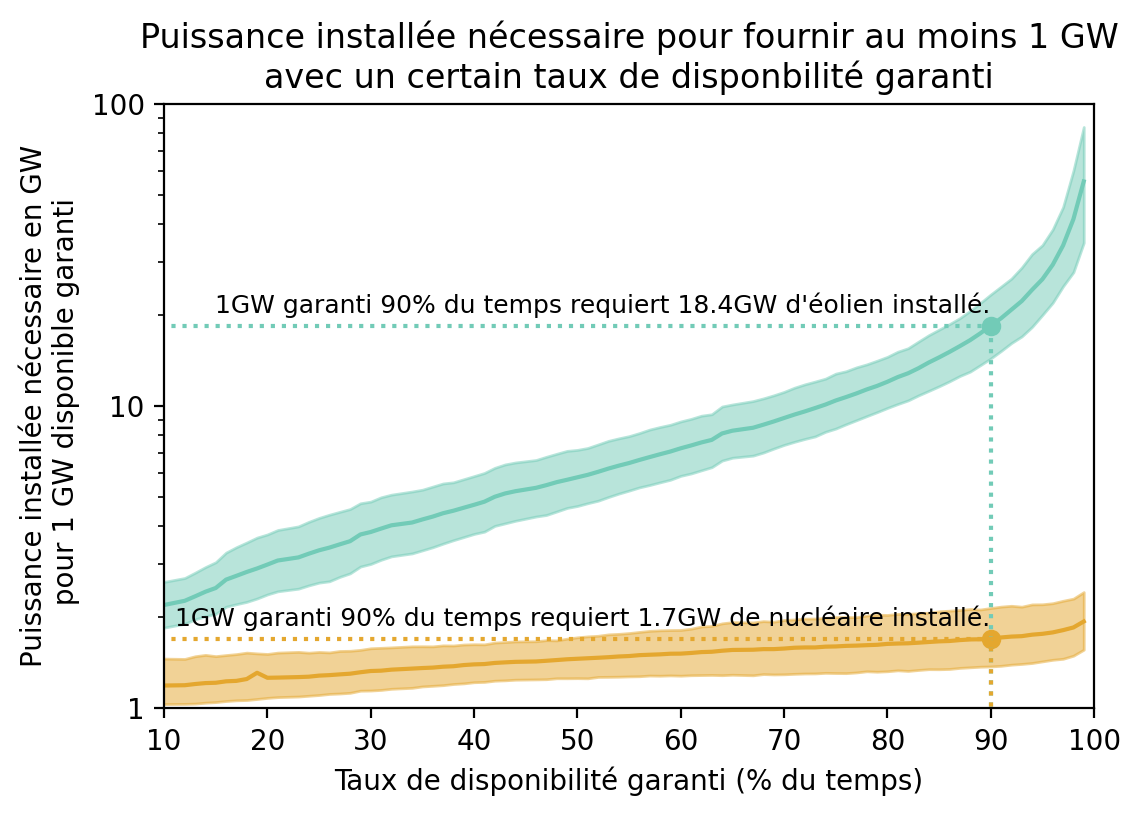
On observe que l’éolien et le nucléaire ont deux comportements très différents. Pour le nucléaire, il suffit d’avoir environ 2 GW installés (soit environ 2 réacteurs) pour garantir 1 GW disponible près de 100% de l’année. Par rapport au critère plus haut, le nucléaire est relativement fiable et donc “non-intermittent”. Pour l’éolien, en revanche, garantir la livraison d’un GW avec une haute disponibilité requière une puissance installée faramineuse. Il faut 18,4 GW pour garantir 1GW dispo 90 % de l’année. Soit typiquement 6000 éoliennes de 3 MW chacune…. À comparer avec les 1,7 réacteurs nécessaires.

Le graphe ci-dessus tient compte de la variabilité de disponibilité du parc d’une année sur l’autre (très mauvaise en ce moment pour le nucléaire), laquelle est représentée par les bandes de couleurs autour des courbes. Même en tenant compte de la faible disponibilité actuelle du parc, donc, il n’y a aucune comparaison entre le nucléaire et l’éolien en terme d’intermittence.

Ci-dessous, le même graphique est produit pour les données correspondant aux mois d’hiver seulement (décembre à mars inclus), où 1) il y a plus de vent et 2) la demande est plus importante, de sorte qu’EDF s’arrange pour que le parc nucléaire soit davantage disponible (et donc que son facteur de charge soit meilleur). On observe bien ces deux effets, car la puissance installée nécessaire dans un cas comme dans l’autre est plus faible. Mais la distinction demeure nette :

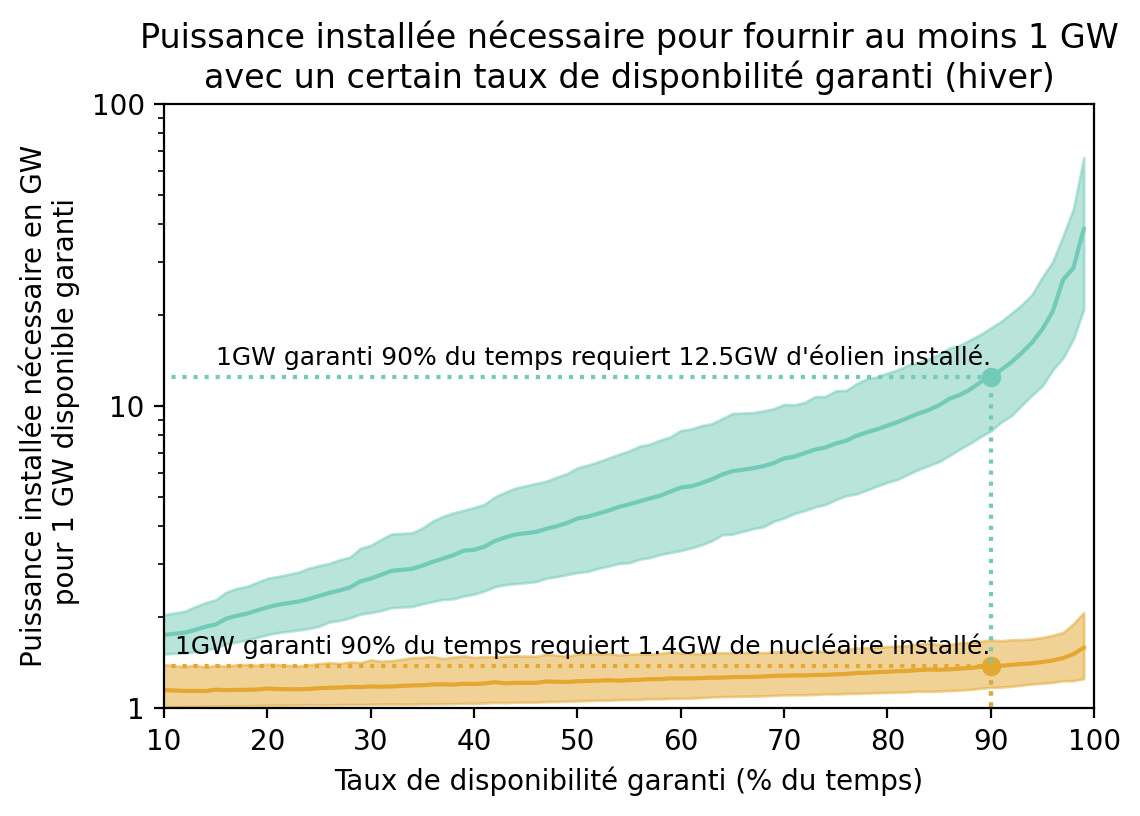
Ces graphiques montrent qu’augmenter la taille du parc éolien terrestre au niveau national pour améliorer la sécurité d’approvisionnement est une très mauvaise stratégie sans capacité de stockage. Ce n’est pas le cas pour le nucléaire, car celui-ci n’est effectivement pas “intermittent”. Le discours de la France Insoumise relève d’une stratégie de communication déconnectée de l’expérience. Si les partis délaissent la réflexion et l’analyse critique au profit de la production de slogans, le débat public s’en portera-t-il vraiment mieux ? Que la France Insoumise affirme que le nucléaire est autant sinon plus intermittent que l’éolien interroge aussi sur la stratégie de sortie du nucléaire envisagée. En effet pour Jean-Luc Mélenchon, “On peut fermer les centrales nucléaires en mettant en face la production d’énergies renouvelables qui correspond” ⁶. Or, comme on le voit sur ces graphes, en aucun cas l’éolien peut apporter la même garantie que le nucléaire et la comparaison est impossible. Si le parc de renouvelables ne couvre pas la demande de manière fiable comme ce sera le cas pour encore longtemps (avant d’avoir suffisamment de surcapacité et de moyens de stockage pour l’absorber), la France Insoumise donnera-t-elle la priorité à la sortie du nucléaire ou à celle des énergies fossiles ?

Méthodologie

Pour produire les graphes ci-dessus, j’ai d’abord dérivé la distribution $\tau(q)$ du facteur de charge défini comme $q(t) = P(t)/P_{\text{inst}}$, i.e. le rapport entre la puissance produite par une certaine filière par rapport à la puissance installée pour cette même filière, lequel est compris entre 0 et 1. $\tau(q)$ est ici défini comme la probabilité que le facteur de charge soit supérieur (ou égal) à $q$ et il est très facile de l’obtenir à partir des données. Par exemple, $\tau(q)=1/2$ signifie que le facteur de charge est plus grand que $q$ la moitié de l’année. Je calcule cette distribution pour chaque année $y$ entre 2012 et 2021, que je note $\tau_y(q)$. La fonction réciproque $q_y(\tau)$ donne, pour un taux de disponibilité donné $\tau$ (par exemple $\tau=$ 90%), le facteur de charge garanti $q(\tau)$. J’ai supposé que $q_y(\tau)$ (le facteur de charge garanti) variait d’une année sur l’autre selon une loi Beta (une distribution de probabilité qui est comprise entre 0 et 1, comme $q$), afin de tenir compte des variations dues aux conditions météorologiques d’une année sur l’autre pour l’éolien, et celles dues, par exemple, aux opérations de maintenance et incidents quelconques pour le nucléaire. Mathématiquement, $q_y(\tau) \sim \text{Beta}(\mu_\tau \eta_\tau, (1-\mu_\tau) \eta_\tau)$, où $\mu_\tau \sim \text{uniform}(0,1)$ est la valeur moyenne attendue et $\eta_\tau \sim \text{Pareto}(1,1.5)$ un paramètre qui contrôle l’ampleur des variations d’une année sur l’autre.

Enfin, les courbes ci-dessus représentent la distribution de l’inverse de $q$ ($\text{1 GW}/q(\tau)$). Les bandes colorées représentent l’intervalle de probabilité à 90%.

Cette méthodologie repose sur la production constatée, laquelle peut-être ajustée en fonction de la demande. Il est probable que la production éolienne soit totalement absorbée, si bien qu’on puisse assimiler le facteur de charge au taux de disponibilité. C’est peut-être moins vrai pour le nucléaire - auquel cas son taux de disponibilité est sous-estimé dans les graphiques ci-dessous.